เนื้อหา

• ที่จะก้าว
• วิธีที่ 1 จาก 3: งานง่ายๆขั้นแรก
• วิธีที่ 2 จาก 3: การคำนวณมูลค่าที่คาดหวังสำหรับผลลัพธ์ที่เฉพาะเจาะจง
• วิธีที่ 3 จาก 3: ทำความเข้าใจแนวคิด
• เคล็ดลับ
• ความจำเป็น

ค่าความคาดหวังเป็นคำทางสถิติและเป็นแนวคิดที่ใช้ในการตัดสินใจว่าการกระทำนั้นจะมีประโยชน์หรือเป็นอันตรายเพียงใด ในการคำนวณมูลค่าที่คาดหวังจำเป็นต้องได้รับความเข้าใจที่ดีเกี่ยวกับผลลัพธ์แต่ละอย่างในสถานการณ์หนึ่ง ๆ และความน่าจะเป็นที่เกี่ยวข้องหรือความน่าจะเป็นที่ผลลัพธ์จะเกิดขึ้น ขั้นตอนด้านล่างนี้เป็นตัวอย่างแบบฝึกหัดเพื่อช่วยให้คุณเข้าใจแนวคิดของค่าความคาดหวัง

ที่จะก้าว

วิธีที่ 1 จาก 3: งานง่ายๆขั้นแรก

1. อ่านแถลงการณ์ ก่อนที่คุณจะเริ่มคิดถึงผลลัพธ์และความน่าจะเป็นที่เป็นไปได้ทั้งหมดสิ่งสำคัญคือคุณต้องเข้าใจปัญหา ตัวอย่างเช่นเกมลูกเต๋าที่มีราคา€ 10 ต่อเกม hex die จะถูกหมุนหนึ่งครั้งและการชนะของคุณขึ้นอยู่กับจำนวนที่คุณหมุน หากทอย 6 คุณจะชนะ€ 30; a 5 ได้รับ€ 20; หมายเลขอื่น ๆ ไม่ให้ผลอะไรเลย
2. แสดงผลลัพธ์ที่เป็นไปได้ทั้งหมด ช่วยในการแสดงผลลัพธ์ที่เป็นไปได้ทั้งหมดในสถานการณ์ที่กำหนด ในตัวอย่างข้างต้นมี 6 ผลลัพธ์ที่เป็นไปได้ เหล่านี้คือ: (1) ม้วน 1 และคุณเสีย 10 เหรียญ (2) ม้วน 2 และคุณเสีย 10 เหรียญ (3) ม้วน 3 และคุณเสีย 10 เหรียญ (4) ม้วน 4 และเสีย 10 เหรียญ , (5) หมุน 5 และรับรางวัล $ 10, (6) หมุน 6 และรับรางวัล $ 20
   • โปรดทราบว่าแต่ละผลลัพธ์จะน้อยกว่าที่อธิบายไว้ข้างต้น 10 ยูโรเนื่องจากคุณจะต้องจ่าย€ 10 ต่อเกมก่อนโดยไม่คำนึงถึงผลลัพธ์
3. กำหนดความน่าจะเป็นของแต่ละผลลัพธ์ ในกรณีนี้ความน่าจะเป็นของ 6 ผลลัพธ์จะเท่ากัน ความน่าจะเป็นของการสุ่มตัวเลขคือ 1 ใน 6 เพื่อให้ง่ายต่อการเขียนเราจะเขียนเศษส่วน (1/6) เป็นทศนิยมโดยใช้เครื่องคิดเลข: 0.167 เขียนความน่าจะเป็นนี้ถัดจากผลลัพธ์แต่ละรายการโดยเฉพาะอย่างยิ่งถ้าคุณต้องการแก้ปัญหาที่มีความน่าจะเป็นที่แตกต่างกันสำหรับแต่ละผลลัพธ์
   • เครื่องคิดเลข 1/6 ของคุณอาจทำบางอย่างเช่น 0.166667 เราปัดเศษเป็น 0.167 เพื่อให้ง่ายต่อการคำนวณโดยไม่ลดทอนความแม่นยำ
   • หากคุณต้องการผลลัพธ์ที่แม่นยำมากอย่าทำให้เป็นทศนิยมเพียงแค่ใส่ 1/6 ลงในสูตรแล้วคำนวณด้วยเครื่องคิดเลขของคุณ
4. บันทึกคุณค่าของแต่ละผลลัพธ์ คูณ $ ของผลลัพธ์ด้วยความน่าจะเป็นที่ผลลัพธ์จะเกิดขึ้นเพื่อคำนวณจำนวนเงินที่ผลลัพธ์จะนำไปสู่มูลค่าที่คาดหวัง ตัวอย่างเช่นผลลัพธ์ของการหมุน 1 คือ - $ 10 และความน่าจะเป็นของการหมุน 1 คือ 0.167 มูลค่าของการขว้าง 1 จึงเท่ากับ (-10) * (0.167)
   • ไม่จำเป็นต้องคำนวณผลลัพธ์เหล่านี้ในตอนนี้หากคุณมีเครื่องคิดเลขที่สามารถดำเนินการหลายอย่างในเวลาเดียวกัน คุณจะได้ผลลัพธ์ที่แม่นยำยิ่งขึ้นหากคุณป้อนสมการทั้งหมด
5. เพิ่มมูลค่าของแต่ละผลลัพธ์เพื่อให้ได้มูลค่าที่คาดหวังของเหตุการณ์ เพื่อดำเนินการตามตัวอย่างข้างต้นค่าความคาดหวังของเกมลูกเต๋าคือ: (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (10 * 0.167) + (20 * 0.167) หรือ - € 1.67 ดังนั้นคุณสามารถคาดหวังว่าจะเสีย $ 1.67 ทุกครั้งในเกมนี้ (ต่อเกม)
6. อะไรคือผลของการคำนวณมูลค่าที่คาดหวัง ในตัวอย่างข้างต้นเราพิจารณาแล้วว่ากำไร (ขาดทุน) ที่คาดหวังจะเป็น - € 1.67 ต่อการโยน นี่เป็นผลลัพธ์ที่เป็นไปไม่ได้สำหรับ 1 เกม คุณสามารถเสีย€ 10 ชนะ€ 10 หรือชนะ€ 20 แต่ในระยะยาวมูลค่าที่คาดหวังคือความน่าจะเป็นโดยเฉลี่ยที่มีประโยชน์ หากคุณเล่นเกมนี้ต่อไปคุณจะเสียเงินโดยเฉลี่ยประมาณ $ 1.67 ต่อเกม อีกวิธีหนึ่งในการคิดเกี่ยวกับมูลค่าที่คาดหวังคือการกำหนดต้นทุน (หรือผลประโยชน์) ให้กับเกม คุณควรเล่นเกมนี้ก็ต่อเมื่อคุณพบว่ามันคุ้มค่าสนุกกับมันมากพอที่จะใช้จ่าย $ 1.67 ทุกครั้ง
   • ยิ่งสถานการณ์เกิดขึ้นซ้ำบ่อยเท่าไหร่ค่าที่คาดหวังก็จะยิ่งถูกต้องมากขึ้นเท่านั้นที่เป็นตัวแทนของผลลัพธ์ที่แท้จริงและเป็นค่าเฉลี่ย ตัวอย่างเช่นคุณอาจเล่นเกม 5 ครั้งติดต่อกันและคุณแพ้ในแต่ละครั้งส่งผลให้สูญเสียเงินเฉลี่ย $ 10 อย่างไรก็ตามหากคุณเล่นเกมมากกว่า 1,000 ครั้งผลการแข่งขันโดยเฉลี่ยจะเข้าใกล้มูลค่าที่คาดไว้ - 1.67 ยูโรต่อเกม หลักการนี้เรียกว่า "กฎแห่งจำนวนมาก"

วิธีที่ 2 จาก 3: การคำนวณมูลค่าที่คาดหวังสำหรับผลลัพธ์ที่เฉพาะเจาะจง

1. ใช้วิธีนี้เพื่อคำนวณจำนวนเหรียญโดยเฉลี่ยที่คุณต้องพลิกก่อนที่จะเกิดรูปแบบใดรูปแบบหนึ่ง ตัวอย่างเช่นคุณสามารถใช้วิธีค้นหาจำนวนเหรียญที่คาดว่าจะพลิกได้จนกว่าคุณจะได้หัวสองครั้งติดต่อกัน ปัญหานี้ค่อนข้างยากกว่าปัญหามาตรฐานเกี่ยวกับค่าความคาดหวังดังนั้นโปรดอ่านส่วนด้านบนของบทความนี้ก่อนหากคุณไม่คุ้นเคยกับแนวคิดเรื่องค่าความคาดหวัง
2. สมมติว่าเรากำลังมองหาค่า x คุณกำลังพยายามกำหนดจำนวนเหรียญที่คุณต้องพลิกโดยเฉลี่ยเพื่อให้ได้สองหัวติดต่อกัน ตอนนี้เราทำการเปรียบเทียบเพื่อหาคำตอบ เราเรียกคำตอบที่เรากำลังมองหา x เราทำการเปรียบเทียบที่จำเป็นทีละขั้นตอน ขณะนี้เรามีสิ่งต่อไปนี้:
   • x = ___
3. ลองนึกดูว่าจะเกิดอะไรขึ้นถ้าการพลิกครั้งแรกสร้างเหรียญ นี่จะเป็นกรณีครึ่งหนึ่งของกรณี หากเป็นกรณีนี้แสดงว่าคุณ "เสีย" ในการพลิกคว่ำในขณะที่โอกาสในการกลิ้งหัวสองครั้งติดต่อกันยังไม่เปลี่ยนแปลง เช่นเดียวกับการโยนเหรียญคาดว่าคุณจะต้องโยนจำนวนครั้งโดยเฉลี่ยก่อนที่จะได้หัวสองครั้งติดต่อกัน กล่าวอีกนัยหนึ่งคุณคาดว่าจะหมุน x จำนวนครั้งรวมทั้งครั้งที่คุณเล่นไปแล้ว ในรูปของสมการ:
   • x = (0.5) (x + 1) + ___
   • เราจะเติมช่องว่างในขณะที่เราคิดเกี่ยวกับสถานการณ์อื่น ๆ ต่อไป
   • คุณสามารถใช้เศษส่วนแทนทศนิยมได้หากง่ายกว่าหรือจำเป็น
4. ลองนึกถึงสิ่งที่เกิดขึ้นเมื่อคุณโยนหัวของคุณ มีโอกาส 0.5 (หรือ 1/2) ที่คุณจะโยนถ้วยในครั้งแรก ดูเหมือนว่าจะเข้าใกล้เป้าหมายของการขว้างศีรษะสองครั้งติดต่อกัน แต่เท่าไหร่? วิธีที่ง่ายที่สุดในการค้นหาคือคิดถึงตัวเลือกของคุณในม้วนที่สอง:
   • หากการโยนครั้งที่สองเป็นเหรียญเราจะกลับไปที่จุดเริ่มต้น
   • ถ้าครั้งที่สองเป็นถ้วยด้วยล่ะก็เสร็จแล้ว!
5. เรียนรู้วิธีคำนวณความน่าจะเป็นที่ทั้งสองเหตุการณ์จะเกิดขึ้น ตอนนี้เรารู้แล้วว่าคุณมีโอกาส 50% ที่คุณจะโยนถ้วย แต่โอกาสที่คุณจะโยนถ้วยสองครั้งติดต่อกันคืออะไร? ในการคำนวณความน่าจะเป็นนี้ให้คูณความน่าจะเป็นของทั้งคู่ ในกรณีนี้คือ 0.5 x 0.5 = 0.25 แน่นอนว่านี่เป็นโอกาสที่คุณจะม้วนหัวแล้วก้อยเพราะทั้งคู่มีโอกาสเกิด 0.5: 0.5 x 0.5 = 0.25
6. เพิ่มผลลัพธ์สำหรับ "หัวแล้วก้อย" ลงในสมการ ตอนนี้เราได้คำนวณความน่าจะเป็นที่เหตุการณ์นี้จะเกิดขึ้นแล้วเราสามารถไปขยายสมการได้ มีโอกาส 0.25 (หรือ 1/4) ที่เราจะเสียการขว้างสองครั้งโดยไม่ก้าวไปข้างหน้า แต่ตอนนี้เรายังต้องการจำนวนการโยนโดยเฉลี่ยเพิ่มขึ้นอีก x เพื่อให้ได้ผลลัพธ์ที่เราต้องการบวกกับ 2 ที่เราโยนไปแล้ว ในรูปแบบสมการสิ่งนี้จะกลายเป็น (0.25) (x + 2) ซึ่งตอนนี้เราสามารถเพิ่มลงในสมการได้:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + ___
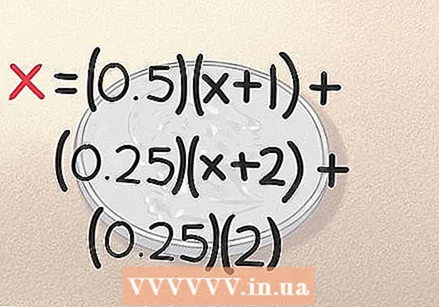7. เพิ่มผลลัพธ์สำหรับ "ส่วนหัวส่วนหัว" ลงในสมการ หากคุณหมุนศีรษะให้มุ่งหน้าด้วยการทอยเหรียญสองครั้งแรกคุณก็เสร็จแล้ว คุณได้ผลลัพธ์ในการขว้าง 2 ครั้ง ดังที่เราได้กล่าวไว้ก่อนหน้านี้มีโอกาส 0.25 ที่จะเกิดขึ้นดังนั้นสมการของสิ่งนี้คือ (0.25) (2) การเปรียบเทียบของเราเสร็จสมบูรณ์แล้ว:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + (0.25) (2)
   • หากคุณไม่แน่ใจว่าคุณได้ไตร่ตรองทุกสถานการณ์ที่เป็นไปได้มีวิธีง่ายๆในการตรวจสอบว่าสมการนั้นสมบูรณ์หรือไม่ ตัวเลขแรกในแต่ละส่วนของสมการแสดงถึงความน่าจะเป็นที่เหตุการณ์จะเกิดขึ้น สิ่งนี้จะรวมได้ถึง 1 เสมอ ตรงนี้ 0.5 + 0.25 + 0.25 = 1 ดังนั้นเราจึงรู้ว่าเราได้รวมทุกสถานการณ์ไว้แล้ว
8. ลดความซับซ้อนของสมการ มาทำให้สมการง่ายขึ้นด้วยการคูณกัน จำไว้ว่าถ้าคุณเห็นบางอย่างในวงเล็บเช่นนี้: (0.5) (x + 1) คุณจะต้องคูณ 0.5 ด้วยแต่ละคำที่อยู่ในวงเล็บชุดที่สอง สิ่งนี้จะให้สิ่งต่อไปนี้: 0.5x + (0.5) (1) หรือ 0.5x + 0.5 ลองทำสิ่งนี้กับแต่ละเทอมในสมการจากนั้นรวมคำศัพท์เหล่านี้เพื่อให้ทุกอย่างดูง่ายขึ้น:
   • x = 0.5x + (0.5) (1) + 0.25x + (0.25) (2) + (0.25) (2)
   • x = 0.5x + 0.5 + 0.25x + 0.5 + 0.5
   • x = 0.75x + 1.5
9. แก้สำหรับ x เช่นเดียวกับสมการใด ๆ คุณจะต้องแยก x ที่ด้านใดด้านหนึ่งของสมการเพื่อคำนวณ จำไว้ว่า x หมายถึง "จำนวนเหรียญโดยเฉลี่ยที่คุณต้องโยนเพื่อให้ได้หัวสองครั้งติดต่อกัน" เมื่อเราคำนวณ x แล้วเราก็พบคำตอบของเราเช่นกัน
   • x = 0.75x + 1.5
   • x - 0.75x = 0.75x + 1.5 - 0.75x
   • 0.25x = 1.5
   • (0.25x) / (0.25) = (1.5) / (0.25)
   • x = 6
   • โดยเฉลี่ยแล้วคุณจะต้องทอยเหรียญ 6 ครั้งก่อนที่จะโยนหัวสองครั้ง

วิธีที่ 3 จาก 3: ทำความเข้าใจแนวคิด

1. มูลค่าที่คาดว่าจะได้รับจริงคืออะไร ค่าความคาดหวังไม่จำเป็นต้องเป็นผลลัพธ์ที่ชัดเจนที่สุดหรือเป็นเหตุเป็นผล บางครั้งค่าความคาดหวังอาจเป็นมูลค่าที่เป็นไปไม่ได้ในสถานการณ์หนึ่ง ๆ ตัวอย่างเช่นมูลค่าความคาดหวังอาจเป็น + 5 ยูโรสำหรับเกมที่มีรางวัลไม่เกิน€ 10 ค่าความคาดหวังบ่งชี้ว่าเหตุการณ์หนึ่ง ๆ มีมูลค่าเท่าใด หากเกมมีมูลค่าที่คาดไว้ + € 5 คุณสามารถเล่นได้หากคุณรู้สึกว่ามันคุ้มค่ากับเวลาและเงินที่คุณจะได้รับต่อเกม หากเกมอื่นมีมูลค่าที่คาดไว้ - $ 20 คุณจะเล่นได้ก็ต่อเมื่อคุณคิดว่าแต่ละเกมมีมูลค่า $ 20
2. เข้าใจแนวคิดของเหตุการณ์ที่เป็นอิสระ ในชีวิตประจำวันพวกเราหลายคนคิดว่าเรามีวันที่โชคดีเมื่อมีสิ่งดีๆเกิดขึ้นและเราคาดหวังว่าวันที่เหลือจะเป็นไปอย่างนั้นในทำนองเดียวกันเราคิดได้ว่าเราประสบอุบัติเหตุมามากพอแล้วและตอนนี้ต้องทำอะไรสนุก ๆ ในทางคณิตศาสตร์สิ่งต่างๆไม่เป็นไปอย่างนั้น หากคุณโยนเหรียญปกติมีโอกาสเหมือนกันที่คุณจะโยนหัวหรือเหรียญ ไม่สำคัญว่าคุณจะโยนไปแล้วกี่ครั้ง ในครั้งต่อไปที่คุณโยนมันยังคงใช้งานได้เหมือนเดิม การโยนเหรียญเป็นแบบ "อิสระ" ของการโยนอื่น ๆ โดยจะไม่ได้รับผลกระทบใด ๆ
   • ความเชื่อที่ว่าคุณจะโชคดีหรือโชคร้ายเมื่อโยนเหรียญ (หรือเกมแห่งโอกาสอื่น ๆ ) หรือ ความจริงที่ว่าความโชคร้ายทั้งหมดของคุณได้สิ้นสุดลงแล้วและโชคก็เข้าข้างคุณเรียกอีกอย่างว่าการโกงของนักพนัน (หรือความเข้าใจผิดของนักพนัน) สิ่งนี้เกี่ยวข้องกับแนวโน้มของผู้คนในการตัดสินใจที่เสี่ยงหรือโง่เขลาเมื่อพวกเขารู้สึกว่าโชคเข้าข้างพวกเขาหรือหากพวกเขารู้สึกว่า "โชคดี" หรือหากพวกเขารู้สึกว่า "โชคกำลังจะพลิกผัน" "
3. เข้าใจกฎหมายจำนวนมาก. คุณอาจคิดว่าค่าความคาดหวังนั้นไม่มีประโยชน์จริงๆเพราะมันแทบไม่ได้บอกคุณว่าผลลัพธ์ที่แท้จริงของสถานการณ์คืออะไร หากคุณคำนวณแล้วว่ามูลค่าที่คาดหวังของเกมรูเล็ตคือ - € 1 และคุณเล่นเกม 3 ครั้งคุณมักจะลงเอยด้วย - 10 ยูโรหรือ + 60 ยูโรหรือผลลัพธ์อื่น ๆ "กฎแห่งตัวเลขจำนวนมาก" ช่วยอธิบายว่าเหตุใดค่าความคาดหวังจึงมีประโยชน์มากกว่าที่คุณคิดยิ่งคุณเล่นมากเท่าไหร่ผลลัพธ์ก็จะยิ่งใกล้เคียงกับความคาดหวังมากเท่านั้น เมื่อคุณดูเหตุการณ์จำนวนมากมีโอกาสดีที่ผลลัพธ์สุดท้ายจะใกล้เคียงกับมูลค่าที่คาดไว้

เคล็ดลับ

• สำหรับสถานการณ์ที่เป็นไปได้หลายผลลัพธ์คุณสามารถสร้างสเปรดชีตในคอมพิวเตอร์เพื่อคำนวณค่าที่คาดหวังโดยใช้ผลลัพธ์และความน่าจะเป็น
• การคำนวณ€ข้างต้นยังทำงานในสกุลเงินอื่น ๆ

ความจำเป็น

• ดินสอ
• กระดาษ
• เครื่องคิดเลข