เนื้อหา

• ขั้นตอน
• วิธีที่ 1 จาก 4: ชุดของทวีคูณ
• วิธีที่ 2 จาก 4: ไพรม์แฟคตอริ่ง
• วิธีที่ 3 จาก 4: การหาตัวหารร่วม
• วิธีที่ 4 จาก 4: อัลกอริทึมของยุคลิด
• เคล็ดลับ

ตัวคูณคือจำนวนที่หารด้วยจำนวนที่ระบุลงตัวตัวคูณร่วมน้อย (LCM) ของกลุ่มตัวเลขคือจำนวนที่น้อยที่สุดที่แต่ละตัวเลขในกลุ่มหารลงตัว ในการหาตัวคูณร่วมน้อย คุณต้องหาตัวประกอบเฉพาะของตัวเลขที่ระบุ LCM สามารถคำนวณได้โดยใช้วิธีอื่นๆ อีกจำนวนหนึ่งที่ใช้กับกลุ่มตัวเลขตั้งแต่สองตัวขึ้นไป

ขั้นตอน

วิธีที่ 1 จาก 4: ชุดของทวีคูณ

1. 1 ดูตัวเลขที่ให้มา วิธีที่อธิบายไว้ในที่นี้ควรใช้ดีที่สุดเมื่อให้ตัวเลขสองตัว ซึ่งแต่ละจำนวนมีค่าน้อยกว่า 10 หากตัวเลขจำนวนมาก ให้ใช้วิธีการอื่น
   • ตัวอย่างเช่น ค้นหาตัวคูณร่วมน้อยของ 5 และ 8 ตัวเลขเหล่านี้เป็นจำนวนน้อย คุณจึงใช้วิธีนี้ได้
2. 2 เขียนชุดตัวเลขที่เป็นจำนวนทวีคูณของจำนวนแรก ตัวคูณคือจำนวนที่หารด้วยจำนวนที่ระบุลงตัว สามารถดูเลขหลายตัวได้ในตารางสูตรคูณ
   • ตัวอย่างเช่น ตัวเลขที่คูณด้วย 5 ได้แก่ 5, 10, 15, 20, 25, 30, 35, 40
3. 3 เขียนชุดตัวเลขที่เป็นจำนวนทวีคูณของจำนวนแรก ทำเช่นนี้ภายใต้ผลคูณของตัวเลขแรกเพื่อเปรียบเทียบตัวเลขสองแถว
   • ตัวอย่างเช่น ตัวเลขที่คูณด้วย 8 ได้แก่ 8, 16, 24, 32, 40, 48, 56 และ 64
4. 4 ค้นหาจำนวนที่น้อยที่สุดที่ปรากฏในทั้งสองแถวของทวีคูณ คุณอาจต้องเขียนชุดยาวของทวีคูณเพื่อหาผลรวม จำนวนที่น้อยที่สุดที่ปรากฏในทั้งสองแถวของทวีคูณคือตัวคูณร่วมที่เล็กที่สุด
   • ตัวอย่างเช่น จำนวนที่น้อยที่สุดที่ปรากฏในชุดผลคูณของ 5 และ 8 คือ 40 ดังนั้น 40 จึงเป็นผลคูณร่วมน้อยของ 5 และ 8

วิธีที่ 2 จาก 4: ไพรม์แฟคตอริ่ง

1. 1 ดูตัวเลขที่ให้มา วิธีที่อธิบายไว้ในที่นี้ควรใช้ดีที่สุดเมื่อให้ตัวเลขสองตัว ซึ่งแต่ละจำนวนมากกว่า 10 หากตัวเลขที่ระบุน้อยกว่า ให้ใช้วิธีการอื่น
   • ตัวอย่างเช่น ค้นหาตัวคูณร่วมน้อยที่ต่ำที่สุดของ 20 และ 84 ตัวเลขแต่ละตัวมีค่ามากกว่า 10 คุณจึงใช้วิธีนี้ได้
2. 2 ปัจจัยออก หมายเลขแรก นั่นคือคุณต้องหาจำนวนเฉพาะดังกล่าวเมื่อคูณกับจำนวนที่กำหนด เมื่อคุณพบปัจจัยเฉพาะแล้ว ให้เขียนเป็นความเท่าเทียมกัน
   • ตัวอย่างเช่น, ${ displaystyle mathbf {2} ครั้ง 10 = 20}$ และ ${ displaystyle mathbf {2} ครั้ง mathbf {5} = 10}$... ดังนั้น ตัวประกอบเฉพาะของ 20 คือ 2, 2 และ 5 เขียนมันเป็นนิพจน์: ${ displaystyle 20 = 2 ครั้ง 2 ครั้ง 5}$.
3. 3 แยกตัวประกอบตัวเลขที่สอง ทำแบบเดียวกับที่คุณแยกตัวประกอบตัวเลขแรก นั่นคือ หาจำนวนเฉพาะที่เมื่อคูณแล้วจะได้ตัวเลขที่กำหนด
   • ตัวอย่างเช่น, ${ displaystyle mathbf {2} ครั้ง 42 = 84}$, ${ displaystyle mathbf {7} ครั้ง 6 = 42}$ และ ${ displaystyle mathbf {3} ครั้ง mathbf {2} = 6}$... ดังนั้น ตัวประกอบเฉพาะของ 84 คือ 2, 7, 3 และ 2 เขียนมันเป็นนิพจน์: ${ displaystyle 84 = 2 ครั้ง 7 ครั้ง 3 ครั้ง 2}$.
4. 4 เขียนปัจจัยร่วมของตัวเลขทั้งสอง เขียนปัจจัยเหล่านี้เป็นการคูณ ในขณะที่คุณจดแต่ละปัจจัย ให้ขีดฆ่าในทั้งสองนิพจน์ (นิพจน์ที่อธิบายการแยกตัวประกอบเฉพาะ)
   • ตัวอย่างเช่น ตัวประกอบร่วมของตัวเลขทั้งสองคือ 2 ดังนั้นเขียน ${ displaystyle 2 ครั้ง}$ และขีดฆ่า 2 ในทั้งสองนิพจน์
   • สามัญของตัวเลขทั้งสองเป็นอีกตัวประกอบของ 2 ดังนั้นเขียน ${ displaystyle 2 ครั้ง 2}$ และขีดฆ่า 2 ตัวที่สองในทั้งสองนิพจน์
5. 5 เพิ่มปัจจัยที่เหลือในการคูณ ปัจจัยเหล่านี้เป็นตัวประกอบที่ไม่ถูกขีดฆ่าในนิพจน์ทั้งสอง กล่าวคือ ตัวประกอบที่ไม่เหมือนกันกับตัวเลขทั้งสอง
   • ตัวอย่างเช่น ในนิพจน์ ${ displaystyle 20 = 2 ครั้ง 2 ครั้ง 5}$ ค่าของ 2 ทั้งสอง (2) ถูกขีดฆ่าเนื่องจากเป็นปัจจัยร่วม ตัวประกอบ 5 ไม่ถูกขีดฆ่า ดังนั้นให้เขียนการคูณดังนี้: ${ displaystyle 2 ครั้ง 2 ครั้ง 5}$
   • ในนิพจน์ ${ displaystyle 84 = 2 ครั้ง 7 ครั้ง 3 ครั้ง 2}$ 2 ทั้งสองถูกขีดฆ่าด้วย (2) ตัวประกอบ 7 และ 3 ไม่ถูกขีดฆ่า ดังนั้นให้เขียนการคูณดังนี้: ${ displaystyle 2 ครั้ง 2 ครั้ง 5 ครั้ง 7 ครั้ง 3}$.
6. 6 คำนวณตัวคูณร่วมน้อย. เมื่อต้องการทำเช่นนี้ ให้คูณตัวเลขในการคูณที่บันทึกไว้
   • ตัวอย่างเช่น, ${ displaystyle 2 ครั้ง 2 ครั้ง 5 ครั้ง 7 ครั้ง 3 = 420}$... ดังนั้นตัวคูณร่วมน้อยของ 20 และ 84 คือ 420

วิธีที่ 3 จาก 4: การหาตัวหารร่วม

1. 1 วาดเส้นตารางสำหรับเกมโอเอกซ์ ตารางดังกล่าวประกอบด้วยเส้นตรงคู่ขนานสองเส้นที่ตัดกัน (ที่มุมฉาก) กับเส้นตรงคู่ขนานอีกสองเส้น ซึ่งจะจบลงด้วยสามแถวและสามคอลัมน์ (ตารางจะคล้ายกับเครื่องหมาย #) เขียนตัวเลขแรกในบรรทัดแรกและคอลัมน์ที่สอง เขียนตัวเลขที่สองในบรรทัดแรกและคอลัมน์ที่สาม
   • ตัวอย่างเช่น ค้นหาตัวคูณร่วมน้อยของ 18 และ 30 เขียน 18 ในแถวแรกและคอลัมน์ที่สอง และเขียน 30 ในแถวแรกและคอลัมน์ที่สาม
2. 2 หาตัวหารร่วมของทั้งสองจำนวน เขียนลงในแถวแรกและคอลัมน์แรก เป็นการดีกว่าที่จะมองหาปัจจัยเฉพาะ แต่นี่ไม่ใช่ข้อกำหนด
   • ตัวอย่างเช่น 18 และ 30 เป็นตัวเลขคู่ ดังนั้นตัวหารร่วมของมันคือ 2 ดังนั้นให้เขียน 2 ในแถวแรกและคอลัมน์แรก
3. 3 หารตัวเลขแต่ละตัวด้วยตัวหารแรก เขียนผลหารแต่ละรายการภายใต้จำนวนที่สอดคล้องกัน ผลหารเป็นผลจากการหารตัวเลขสองตัว
   • ตัวอย่างเช่น, ${ displaystyle 18 div 2 = 9}$ดังนั้นเขียน 9 ภายใต้ 18
   • ${ displaystyle 30 div 2 = 15}$ดังนั้นเขียน 15 ภายใต้ 30
4. 4 หาตัวหารร่วมของผลหารทั้งสอง หากไม่มีตัวหารดังกล่าว ให้ข้ามสองขั้นตอนถัดไป มิฉะนั้น ให้เขียนตัวหารในแถวที่สองและคอลัมน์แรก
   • ตัวอย่างเช่น 9 และ 15 หารด้วย 3 ลงตัว ดังนั้นให้เขียน 3 ในแถวที่สองและคอลัมน์แรก
5. 5 หารผลหารแต่ละรายการด้วยตัวประกอบที่สอง เขียนผลหารแต่ละผลหารภายใต้ผลหารที่สอดคล้องกัน
   • ตัวอย่างเช่น, ${ displaystyle 9 div 3 = 3}$ดังนั้นเขียน 3 ภายใต้ 9
   • ${ displaystyle 15 div 3 = 5}$ดังนั้นเขียน 5 ภายใต้ 15
6. 6 หากจำเป็น ให้เสริมกริดด้วยเซลล์เพิ่มเติม ทำซ้ำขั้นตอนที่อธิบายไว้จนกว่าผลหารจะมีตัวหารร่วม
7. 7 วงกลมตัวเลขในคอลัมน์แรกและแถวสุดท้ายของตาราง จากนั้นจดตัวเลขที่เลือกไว้เป็นการคูณ
   • ตัวอย่างเช่น หมายเลข 2 และ 3 อยู่ในคอลัมน์แรก และหมายเลข 3 และ 5 อยู่ในแถวสุดท้าย ดังนั้นให้เขียนการคูณดังนี้: ${ displaystyle 2 ครั้ง 3 ครั้ง 3 ครั้ง 5}$.
8. 8 หาผลการคูณเลข. การดำเนินการนี้จะคำนวณผลคูณร่วมน้อยของตัวเลขทั้งสองที่ระบุ
   • ตัวอย่างเช่น, ${ displaystyle 2 ครั้ง 3 ครั้ง 3 ครั้ง 5 = 90}$... ดังนั้นตัวคูณร่วมน้อยของ 18 และ 30 คือ 90

วิธีที่ 4 จาก 4: อัลกอริทึมของยุคลิด

1. 1 จำคำศัพท์ที่เกี่ยวข้องกับการดำเนินการหาร เงินปันผลคือจำนวนที่จะถูกหาร ตัวหารคือจำนวนที่หารด้วย ผลหารเป็นผลจากการหารตัวเลขสองตัว ส่วนที่เหลือคือจำนวนที่เหลือเมื่อหารสองตัวเลข
   • ตัวอย่างเช่น ในนิพจน์ ${ displaystyle 15 div 6 = 2}$ ost. 3:
     15 คือเงินปันผล
     6 เป็นตัวหาร
     2 คือผลหาร
     3 คือส่วนที่เหลือ
2. 2 เขียนนิพจน์ที่อธิบายการหารที่เหลือ การแสดงออก: ${ displaystyle { text {dividend}} = { text {divisor}} ครั้ง { text {quotient}} + { text {remainder}}}$... นิพจน์นี้จะใช้ในการเขียนอัลกอริธึมของ Euclid และค้นหาตัวหารร่วมมากของตัวเลขสองตัว
   • ตัวอย่างเช่น, ${ displaystyle 15 = 6 ครั้ง 2 + 3}$.
   • ตัวหารร่วมที่ยิ่งใหญ่ที่สุด (GCD) คือจำนวนที่มากที่สุดโดยที่ตัวเลขที่กำหนดทั้งหมดนั้นหารลงตัว
   • ในวิธีนี้ คุณต้องหาตัวประกอบร่วมที่มากที่สุดก่อนแล้วจึงคำนวณตัวคูณร่วมน้อย
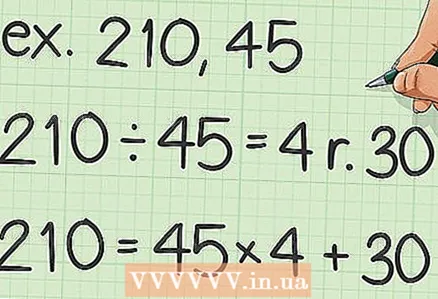3. 3 ถือว่าตัวเลขที่มากกว่าทั้งสองเป็นเงินปันผล พิจารณาจำนวนที่น้อยกว่าของทั้งสองเป็นตัวหาร สำหรับตัวเลขเหล่านี้ ให้เขียนนิพจน์ที่อธิบายการหารที่เหลือ
   • ตัวอย่างเช่น ค้นหาตัวคูณร่วมน้อยของ 210 และ 45 เขียนนิพจน์นี้: ${ displaystyle 210 = 45 ครั้ง 4 + 30}$.
4. 4 เปลี่ยนตัวหารแรกเป็นเงินปันผลใหม่ ใช้เศษที่เหลือเป็นตัวหารใหม่ สำหรับตัวเลขเหล่านี้ ให้เขียนนิพจน์ที่อธิบายการหารที่เหลือ
   • ตัวอย่างเช่น, ${ displaystyle 45 = 30 ครั้ง 2 + 15}$.
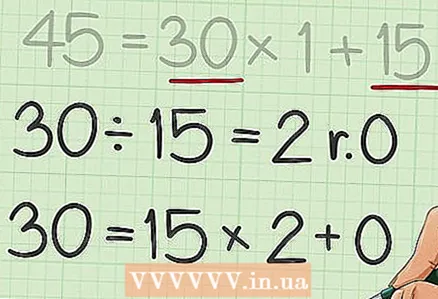5. 5 ทำซ้ำขั้นตอนที่อธิบายไว้จนกว่าส่วนที่เหลือจะเท่ากับ 0 ใช้ตัวหารก่อนหน้าเป็นตัวหารใหม่ และตัวหารก่อนหน้าเป็นตัวหารใหม่ จดนิพจน์ที่เหมาะสมสำหรับตัวเลขเหล่านี้
   • ตัวอย่างเช่น, ${ displaystyle 30 = 15 ครั้ง 2 + 0}$... เนื่องจากส่วนที่เหลือเป็น 0 คุณจึงไม่สามารถหารเพิ่มเติมได้
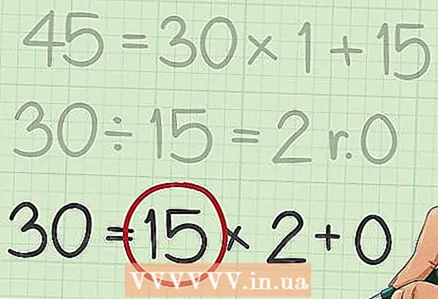6. 6 ดูตัวหารสุดท้าย. นี่คือตัวหารร่วมมากของจำนวนสองตัว
   • ตัวอย่างเช่น นิพจน์สุดท้ายคือ ${ displaystyle 30 = 15 ครั้ง 2 + 0}$ตัวหารสุดท้ายคือ 15 ดังนั้น 15 เป็นตัวหารร่วมมากของ 210 และ 45
7. 7 คูณสองตัวเลข จากนั้นหารผลคูณด้วยตัวประกอบร่วมที่ยิ่งใหญ่ที่สุด วิธีนี้จะคำนวณผลคูณร่วมน้อยของตัวเลขสองตัว [[[รูปภาพ: ค้นหาตัวคูณร่วมน้อยของตัวเลขสองตัวขั้นตอนที่ 25.webp | ศูนย์]]
   • ตัวอย่างเช่น, ${ displaystyle 210 ครั้ง 45 = 9450}$... หารผลลัพธ์ด้วย GCD: ${ displaystyle { frac {9450} {15}} = 630}$... ดังนั้น 630 จึงเป็นตัวคูณร่วมน้อยของ 210 และ 45

เคล็ดลับ

• หากคุณต้องการค้นหา LCM ของตัวเลขสามตัวขึ้นไป ให้ทำให้ง่ายสำหรับตัวคุณเอง ตัวอย่างเช่น ในการหา LCM ของ 16, 20 และ 32 ขั้นแรกให้ค้นหาตัวคูณร่วมน้อยของ 16 และ 20 (ซึ่งก็คือ 80) จากนั้นให้หา LCM ที่ 80 และ 32 ซึ่งก็คือ 160
• LCM มีประโยชน์หลายอย่าง ตัวอย่างเช่น ในการบวกหรือลบเศษส่วน จะต้องมีตัวส่วนเหมือนกัน หากเศษส่วนมีตัวส่วนต่างกัน คุณต้องแปลงเศษส่วนเพื่อนำมาเป็นตัวส่วนร่วม และนี่จะทำได้ง่ายกว่าถ้าคุณหาตัวส่วนร่วมที่เล็กที่สุด, ซึ่งเท่ากับผลคูณร่วมที่เล็กที่สุดของตัวเลขที่อยู่ในตัวส่วนของเศษส่วน.