เนื้อหา

• ขั้นตอน
• คำแนะนำ

ความแปรปรวนจะวัดการกระจายของชุดข้อมูล มีประโยชน์มากในการสร้างแบบจำลองทางสถิติ: ความแปรปรวนต่ำอาจเป็นตัวบ่งชี้ว่าคุณกำลังอธิบายข้อผิดพลาดหรือสัญญาณรบกวนแบบสุ่มแทนที่จะเป็นความสัมพันธ์พื้นฐานในข้อมูล บทความนี้ wikiHow จะแนะนำวิธีการคำนวณความแปรปรวน

ขั้นตอน

วิธีที่ 1 จาก 2: คำนวณความแปรปรวนของตัวอย่าง

1. 

   เขียนชุดข้อมูลตัวอย่างของคุณ ในกรณีส่วนใหญ่นักสถิติจะมีข้อมูลเกี่ยวกับกลุ่มตัวอย่างหรือกลุ่มย่อยของประชากรที่พวกเขากำลังศึกษาอยู่เท่านั้น ตัวอย่างเช่นแทนที่จะใช้การวิเคราะห์ทั่วไปเกี่ยวกับ "ราคาของรถยนต์ทุกคันในเยอรมนี" นักสถิติอาจพบว่าค่าใช้จ่ายของตัวอย่างสุ่มไม่กี่พันคัน นักสถิติสามารถใช้ตัวอย่างนี้เพื่อประเมินราคารถยนต์ในเยอรมนีได้ดี อย่างไรก็ตามมีแนวโน้มว่าจะไม่ตรงกับตัวเลขจริง
   • ตัวอย่างเช่น: เมื่อวิเคราะห์จำนวนมัฟฟินที่ขายได้ต่อวันที่ร้านกาแฟคุณได้สุ่มตัวอย่างหกวันและได้ผลลัพธ์ดังนี้ 38, 37, 36, 28, 18, 14, 12, 11, 10.7, 9.9 นี่คือตัวอย่างไม่ใช่ประชากรเนื่องจากคุณไม่มีข้อมูลสำหรับทุกวันที่ร้านเปิด
   • ถ้า ทุก จุดข้อมูลในต้นแบบโปรดไปที่วิธีการด้านล่าง

2. 

   
   
   จดสูตรความแปรปรวนของตัวอย่าง ความแปรปรวนของชุดข้อมูลบ่งชี้ระดับการกระจายของจุดข้อมูล ยิ่งความแปรปรวนเข้าใกล้ศูนย์มากเท่าไหร่จุดข้อมูลก็จะยิ่งถูกจัดกลุ่มมากขึ้นเท่านั้น เมื่อทำงานกับชุดข้อมูลตัวอย่างให้ใช้สูตรต่อไปนี้เพื่อคำนวณความแปรปรวน:
   • = /_{(n - 1)}
   • คือความแปรปรวน ความแปรปรวนจะคำนวณเป็นหน่วยกำลังสองเสมอ
   • แทนค่าในชุดข้อมูลของคุณ
   • ∑ หมายถึง "ผลรวม" บอกให้คุณคำนวณพารามิเตอร์ต่อไปนี้สำหรับแต่ละค่าแล้วบวกเข้าด้วยกัน
   • x̅คือค่าเฉลี่ยของตัวอย่าง
   • n คือจำนวนจุดข้อมูล

3. 

   
   
   คำนวณค่าเฉลี่ยของกลุ่มตัวอย่าง. สัญลักษณ์x̅หรือ "x-horizontal" ใช้เพื่อระบุค่าเฉลี่ยของกลุ่มตัวอย่าง คำนวณตามที่คุณต้องการโดยเฉลี่ย: รวมจุดข้อมูลทั้งหมดแล้วหารด้วยจำนวนจุด
   • ตัวอย่างเช่น: ขั้นแรกเพิ่มจุดข้อมูลของคุณ: 17 + 15 + 23 + 7 + 9 + 13 = 84
     จากนั้นหารผลลัพธ์ด้วยจำนวนจุดข้อมูลในกรณีนี้คือ 6: 84 ÷ 6 = 14
     ค่าเฉลี่ยตัวอย่าง = x̅ = 14.
   • คุณสามารถคิดว่าค่าเฉลี่ยเป็น "จุดศูนย์กลาง" ของข้อมูล หากข้อมูลอยู่กึ่งกลางรอบค่าเฉลี่ยความแปรปรวนจะต่ำ หากกระจายอยู่ไกลจากค่าเฉลี่ยความแปรปรวนจะสูง

4. 

   
   
   ลบค่าเฉลี่ยออกจากจุดข้อมูลแต่ละจุด ตอนนี้เป็นเวลาคำนวณ - x̅โดยแต่ละจุดในชุดข้อมูลของคุณคือ ผลลัพธ์แต่ละรายการจะบ่งบอกถึงการเบี่ยงเบนจากค่าเฉลี่ยของแต่ละจุดที่เกี่ยวข้องหรือระบุระยะทางจากจุดนั้นถึงค่าเฉลี่ย
   • ตัวอย่างเช่น:
     - x̅ = 17 - 14 = 3
     - x̅ = 15 - 14 = 1
     - x̅ = 23 - 14 = 9
     - x̅ = 7 - 14 = -7
     - x̅ = 9 - 14 = -5
     - x̅ = 13 - 14 = -1
   • มันง่ายมากที่จะตรวจสอบการคำนวณของคุณเนื่องจากผลลัพธ์จะต้องรวมเป็นศูนย์นั่นเป็นเพราะค่าเฉลี่ยของผลลัพธ์ที่เป็นลบ (ระยะห่างจากค่าเฉลี่ยถึงตัวเลขเล็ก ๆ ) ผลลัพธ์ที่เป็นบวก (ระยะห่างจากค่าเฉลี่ยถึงตัวเลขที่มากขึ้น) จะถูกตัดออกอย่างสมบูรณ์

5. 

   ยกกำลังสองผลลัพธ์ทั้งหมด ตามที่ระบุไว้ข้างต้นรายการค่าเบี่ยงเบนปัจจุบัน (- x̅) มีผลรวมเป็นศูนย์นั่นหมายความว่า "ค่าเบี่ยงเบนเฉลี่ย" จะเป็นศูนย์เสมอและไม่มีอะไรสามารถพูดได้เกี่ยวกับการกระจายของข้อมูล เพื่อแก้ปัญหานี้เราจะพบค่ากำลังสองของส่วนเบี่ยงเบนแต่ละตัว ด้วยเหตุนี้ทั้งหมดจึงเป็นจำนวนบวกค่าลบและค่าบวกจะไม่ตัดกันอีกต่อไปและให้ผลรวมเป็นศูนย์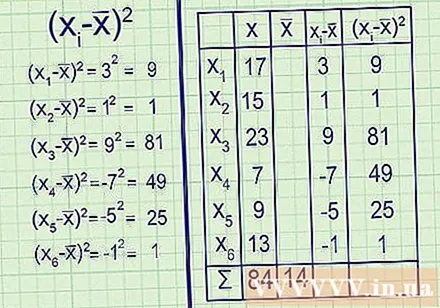
   • ตัวอย่างเช่น:
     (- x̅)
     - x̅)
     9 = 81
     (-7) = 49
     (-5) = 25
     (-1) = 1
   • ตอนนี้คุณมี (- x̅) สำหรับแต่ละจุดข้อมูลในตัวอย่าง

6. 

   หาผลรวมของค่ากำลังสอง ตอนนี้เป็นเวลาคำนวณตัวเศษทั้งหมดของสูตร: ∑ ไซโคลขนาดใหญ่ ∑ กำหนดให้คุณต้องเพิ่มค่าองค์ประกอบต่อไปนี้สำหรับแต่ละค่า คุณได้คำนวณ (- x̅) สำหรับแต่ละค่าในตัวอย่างแล้วสิ่งที่คุณต้องทำก็แค่เพิ่มผลลัพธ์เข้าด้วยกัน
   • ตัวอย่างเช่น: 9 + 1 + 81 + 49 + 25 + 1 = 166.

7. 

   หารด้วย n - 1 โดยที่ n คือจำนวนจุดข้อมูล เมื่อนานมาแล้วเมื่อคำนวณความแปรปรวนตัวอย่างนักสถิติจะหารด้วย n เท่านั้น การหารนั้นจะให้ค่าเฉลี่ยของส่วนเบี่ยงเบนกำลังสองซึ่งตรงกับความแปรปรวนของตัวอย่างนั้นทุกประการ อย่างไรก็ตามโปรดทราบว่ากลุ่มตัวอย่างเป็นเพียงการประมาณของประชากรกลุ่มใหญ่เท่านั้น หากคุณสุ่มตัวอย่างอื่นและทำการคำนวณแบบเดียวกันคุณจะได้ผลลัพธ์ที่แตกต่างกัน ปรากฎว่าการหารด้วย n -1 แทนที่จะเป็น n ช่วยให้คุณสามารถประมาณค่าความแปรปรวนของประชากรจำนวนมากได้ดีขึ้นซึ่งคุณสนใจจริงๆ การแก้ไขนี้เป็นเรื่องปกติมากจนปัจจุบันเป็นนิยามที่ยอมรับของความแปรปรวนตัวอย่าง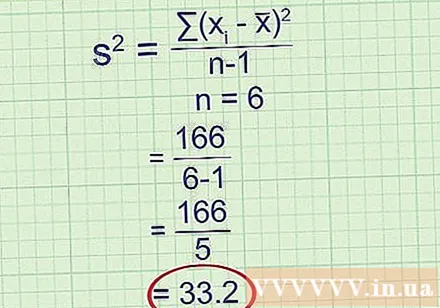
   • ตัวอย่างเช่น: มีจุดข้อมูลหกจุดในตัวอย่างดังนั้น n = 6
     ความแปรปรวนตัวอย่าง = 33,2

8. 

   ทำความเข้าใจเกี่ยวกับความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน โปรดทราบว่าเนื่องจากมีอำนาจในสูตรจึงวัดความแปรปรวนเป็นกำลังสองของหน่วยของข้อมูลต้นฉบับ นี่เป็นภาพที่สับสน แต่บ่อยครั้งค่าเบี่ยงเบนมาตรฐานมีประโยชน์มาก แต่ไม่มีประเด็นให้เสียความพยายามใด ๆ เนื่องจากค่าเบี่ยงเบนมาตรฐานถูกกำหนดโดยรากที่สองของความแปรปรวน นั่นเป็นเหตุผลที่ความแปรปรวนของตัวอย่างถูกเขียนเป็นเงื่อนไขและส่วนเบี่ยงเบนมาตรฐานของตัวอย่างคือ
   • ตัวอย่างเช่นค่าเบี่ยงเบนมาตรฐานของตัวอย่างข้างต้น = s = √33.2 = 5.76
   โฆษณา

วิธีที่ 2 จาก 2: คำนวณความแปรปรวนของประชากร

1. 

   เริ่มต้นด้วยชุดข้อมูลหลัก คำว่า "ประชากร" ใช้เพื่ออ้างถึงข้อสังเกตที่เกี่ยวข้องทั้งหมด ตัวอย่างเช่นหากคุณกำลังศึกษาอายุของชาวฮานอยประชากรโดยรวมของคุณจะรวมอายุของทุกคนที่อาศัยอยู่ในฮานอย โดยปกติคุณจะสร้างสเปรดชีตสำหรับชุดข้อมูลขนาดใหญ่เช่นนี้ แต่นี่คือชุดข้อมูลตัวอย่างขนาดเล็ก:
   • ตัวอย่างเช่น: ในห้องของพิพิธภัณฑ์สัตว์น้ำมีตู้ปลาหกตัว ถังทั้งหกนี้มีจำนวนปลาดังต่อไปนี้:
     
     
     
     
     
     

2. 

   เขียนสูตรสำหรับความแปรปรวนโดยรวม เนื่องจากประชากรมีข้อมูลทั้งหมดที่เราต้องการสูตรนี้จึงให้ความแปรปรวนที่แน่นอนของประชากร เพื่อแยกความแตกต่างจากความแปรปรวนตัวอย่าง (ซึ่งเป็นเพียงการประมาณเท่านั้น) นักสถิติใช้ตัวแปรอื่น:
   • σ = /_n
   • σ = ความแปรปรวนตัวอย่าง นี่คือไส้กรอกกำลังสองตามปกติ ความแปรปรวนวัดเป็นหน่วยกำลังสอง
   • แสดงถึงองค์ประกอบในชุดข้อมูลของคุณ
   • องค์ประกอบใน ∑ ถูกคำนวณสำหรับแต่ละค่าจากนั้นจึงรวมเข้าด้วยกัน
   • μคือค่าเฉลี่ยโดยรวม
   • n คือจำนวนจุดข้อมูลในประชากร

3. 

   ค้นหาค่าเฉลี่ยของประชากร เมื่อวิเคราะห์ประชากรสัญลักษณ์μ ("mu") แสดงถึงค่าเฉลี่ยเลขคณิต หากต้องการหาค่าเฉลี่ยให้บวกจุดข้อมูลทั้งหมดแล้วหารด้วยจำนวนจุด
   • คุณสามารถคิดค่าเฉลี่ยเป็น "ค่าเฉลี่ย" ได้ แต่โปรดระวังเพราะคำนี้มีคำจำกัดความทางคณิตศาสตร์มากมาย
   • ตัวอย่างเช่น: ค่าเฉลี่ย = μ = = 10,5

4. 

   ลบค่าเฉลี่ยออกจากจุดข้อมูลแต่ละจุด จุดข้อมูลที่อยู่ใกล้ค่าเฉลี่ยจะมีความแตกต่างใกล้เคียงกับศูนย์มากขึ้น ทำซ้ำปัญหาการลบสำหรับจุดข้อมูลทั้งหมดและคุณอาจจะเริ่มรู้สึกถึงการกระจายของข้อมูล
   • ตัวอย่างเช่น:
     - μ = 5 – 10,5 = -5,5
     - μ = 5 – 10,5 = -5,5
     - μ = 8 – 10,5 = -2,5
     - μ = 12 - 10., = 1,5
     - μ = 15 – 10,5 = 4,5
     - μ = 18 – 10,5 = 7,5

5. 

   สี่เหลี่ยมแต่ละป้าย ณ จุดนี้ผลลัพธ์บางอย่างที่ได้รับจากขั้นตอนก่อนหน้าจะเป็นลบและบางส่วนจะเป็นบวกหากต้องการแสดงข้อมูลบนเส้นสามมิติทั้งสองรายการนี้จะแสดงตัวเลขทางซ้ายและขวาของค่าเฉลี่ย สิ่งนี้จะไม่มีประโยชน์ในการคำนวณความแปรปรวนเนื่องจากทั้งสองกลุ่มนี้จะยกเลิกซึ่งกันและกัน ให้ยกกำลังสองทั้งหมดเพื่อให้เป็นบวกทั้งหมด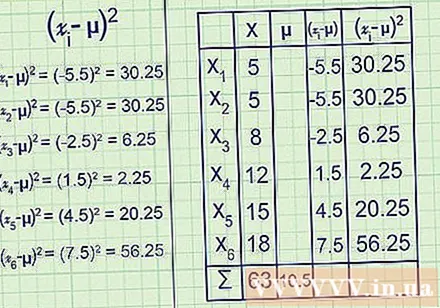
   • ตัวอย่างเช่น:
     (- μ) สำหรับแต่ละค่าของ ผม ทำงานตั้งแต่ 1 ถึง 6:
     (-5,5) = 30,25
     (-5,5) = 30,25
     (-2,5) = 6,25
     (1,5) = 2,25
     (4,5) = 20,25
     (7,5) = 56,25

6. 

   หาค่าเฉลี่ยของผลลัพธ์ของคุณ ตอนนี้คุณมีค่าสำหรับจุดข้อมูลแต่ละจุดซึ่งสัมพันธ์กัน (ไม่ใช่โดยตรง) ว่าจุดข้อมูลนั้นอยู่ห่างจากค่าเฉลี่ยเท่าใด เฉลี่ยโดยการบวกเข้าด้วยกันแล้วหารด้วยจำนวนค่าที่คุณมี
   • ตัวอย่างเช่น:
     ความแปรปรวนโดยรวม = 24,25

7. 

   ติดต่อสูตร. หากคุณไม่แน่ใจว่าวิธีนี้เหมาะกับสูตรที่อธิบายไว้ตอนต้นของวิธีการอย่างไรให้เขียนปัญหาทั้งหมดลงด้วยมือและอย่าย่อ: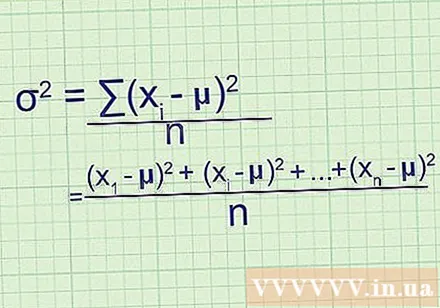
   • หลังจากพบความแตกต่างจากค่าเฉลี่ยและกำลังสองคุณจะได้ (- μ) (- μ) และอื่น ๆ จนถึง (- μ) จุดข้อมูลสุดท้ายอยู่ที่ไหน ในชุดข้อมูล
   • ในการหาค่าเฉลี่ยของค่าเหล่านี้ให้บวกเข้าด้วยกันแล้วหารด้วย n: ((- μ) + (- μ) + ... + (- μ)) / n
   • หลังจากเขียนตัวเศษใหม่ด้วยสัญกรณ์ sigmoid คุณมี /_n, ความแปรปรวนของสูตร
   โฆษณา

คำแนะนำ

• เนื่องจากความแปรปรวนเป็นเรื่องยากที่จะตีความค่านี้จึงมักถูกคำนวณเป็นจุดเริ่มต้นในการหาค่าเบี่ยงเบนมาตรฐาน
• การใช้ "n-1" แทน "n" ในตัวส่วนเมื่อวิเคราะห์ตัวอย่างเป็นเทคนิคที่เรียกว่าการแก้ไขเบสเซล กลุ่มตัวอย่างเป็นเพียงค่าประมาณของประชากรทั้งหมดและค่าเฉลี่ยตัวอย่างมีความเอนเอียงบางอย่างที่ตรงกับค่าประมาณนั้น การแก้ไขนี้ช่วยขจัดอคติข้างต้น มันเกี่ยวข้องกับข้อเท็จจริงที่ว่าเมื่อมีการแจกแจงจุดข้อมูล n - 1 จุดสุดท้ายแล้ว n เป็นค่าคงที่อยู่แล้วเนื่องจากมีเพียงค่าบางค่าเท่านั้นที่ใช้ในการคำนวณค่าเฉลี่ยของตัวอย่าง (x̅) ในสูตรความแปรปรวน